Wolfendale System
Worked Example - Stage 2
Stage 2 - Whole Process
Now that all the seats in a particular electorate have been assigned let's look at the national perspective in Stage 2. We shall assume Case 2 from the above section was the actual result from the previous stage, and we shall assume that the total size of parliament is 175 to ensure no loss of members relative to the current example in Australia. Further we shall assume that the national electorate % votes reflect those of this seat exactly.
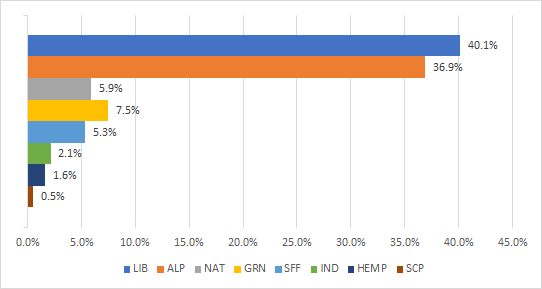
This Produces the following table of expected results:
Note: As per the description of the system above, only parties with >4% may be elected unless they were successful at winning a seat in Stage 1.
Let us assume that the actual seats acquired were as follows:
LIB = 75 - 42.9%
ALP = 69 - 39.4%
NAT = 11 - 6.3%
GRN = 14 - 8.0%
IND = 2 - 1.1%
HEMP = 3 - 1.7%
SCP = 1 - 0.6%
A single seat has a weighting of ~0.57% a party whose representation % is below their vote % by more than that is ‘under-represented’. As is any party with >4% of the vote who has gained no seats. In this case SFF is under-represented on account of having 0 seats and >4% of the vote.
Step 1:
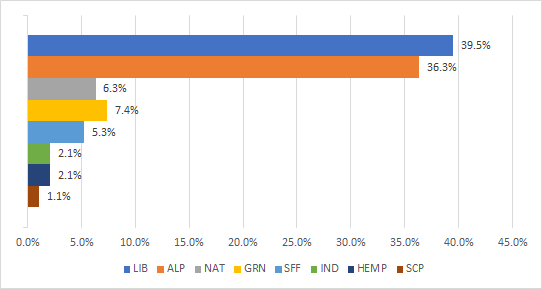
We begin with this representation of the initial data set above:
SFF is underrepresented by 5.3%. This is equivalent to ~9.3 seats. In order to minimise the likelihood of reassignation on a second round they are assigned 10 seats (it rounds up).
SFF’s lack of representation above the threshold has thus been resolved.
Step 2:
We now look at who is underrepresented by >1 member of the floating total. As you add more elected members the % that each one represents drops below the ~0.57%. Setting the threshold at a fixed position ensures with mathematical certainty that the process of improving representation winds down to a point in a minimal amount of time, but lowers the final representativeness. A fixed threshold is recommended for governments with <150 members, but this example shall use the floating threshold.
IND and HEMP are underrepresented but IND is more underrepresented so they receive the first additional member. Further they are still the most underrepresented and will receive the second additional member too:
HEMP and SCP are now up for members but HEMP is more so:
SCP and NAT are now up for members but SCP is more so:
Only NAT is up for a member:
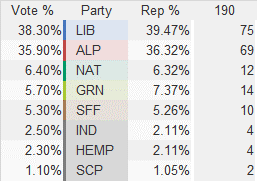
At this point no one is below the threshold for being underrepresented and the final government looks like this:
The total government size is 190 members and the proportion of members is listed under “Rep %”, which may be contrasted with “Vote %” from the primary vote.
The significance of local constituency victories remain weighted very slightly higher but no party of significance in the public mind is excluded by more than the weighting of a single member.